前十名日系养成游戏排行榜2022 人气最高日系养成游戏合集由网友冯克安收集自网络。
前十名日系养成游戏排行榜2022 人气最高日系养成游戏合集
不少小伙伴特别喜欢玩养成,觉得角色在自己手上慢慢成长起来是一件很有成就感的事情,今天就给大家带来十大日系养成游戏排行榜2022。这些游戏不仅可以养成不同的角色,风格还是日系的,更加引人喜爱画面也更加好看,角色形象刻画萌化人心,感兴趣的小伙伴快来看看吧。
1、《世界弹射物语》
每一个人物都是厉害的弹射高手,只要瞄准好以后就能发生小炮弹,可爱的像素风格加上日系的角色形象,让游戏看起来极具童趣,想要发挥更强的战斗力还要做好阵容搭配。

2、《战双帕弥什》
不管是末世题材还是养成仿生人,每一个都踩在玩家的热点上,并且仿生人还是日系的美少女,看起来又飒又可爱,里面含有大量的动作战斗,这些战斗都是为了保护地球。

3、《阴阳师》
回合制的设定让小伙伴可以尽情观赏这些日系妖怪战斗的飒爽英姿,虽然技能是规定的,也不需要小伙伴有太多的操作,但是每一场战斗都非常燃,妖怪的形象也很吸引人。

4、《深空之眼》
画面品质非常高,这样小伙伴可以更近距离欣赏角色的每一个动态和静态,角色养成有非常多的线路,想要在战斗的时候把技能衔接流畅,需要大家提高一下操作技术。

5、《灵魂潮汐》
这一次小伙伴将和日系的美少女人偶们一起到地下迷宫去探险,进入迷宫以后只有正确的走位才能触发机关或者隐藏地图,每一步都要走得小心翼翼。
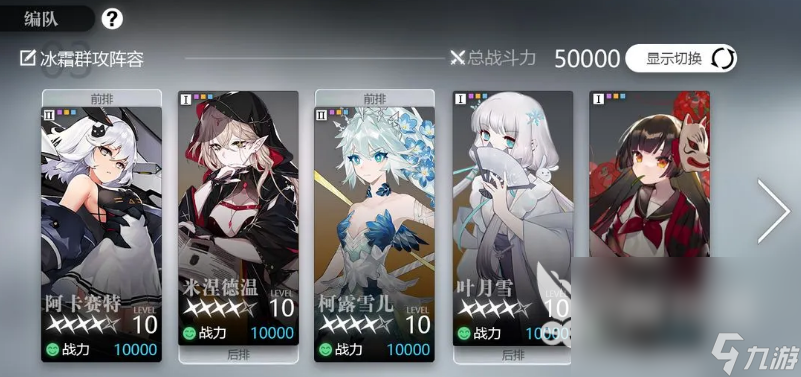
6、《碧蓝航线》
可以打即时的海战,也能养成各种风格的战舰娘,可以单独作战,如果有朋友一起玩的话也可以双排去打海战,这样在战术的配合上就可以更加默契了。

7、《少女前线云图计划》
不管是养成部分还是战斗部分都很考验策略,因为战斗的时候是需要组建阵容的,如何在前期就能利用有限的资源来培养出一个过渡阵容是小伙伴需要好好琢磨的事情。

8、《坎特伯雷公主与骑士唤醒冠军之剑的奇幻冒险》
玩法十分新颖,每个英雄都有自己的专属消除方式,有些是三消,有些则是给其他的英雄来造方块,只要阵容搭配得好,消快的速度就会提上来,伤害也大大增加。
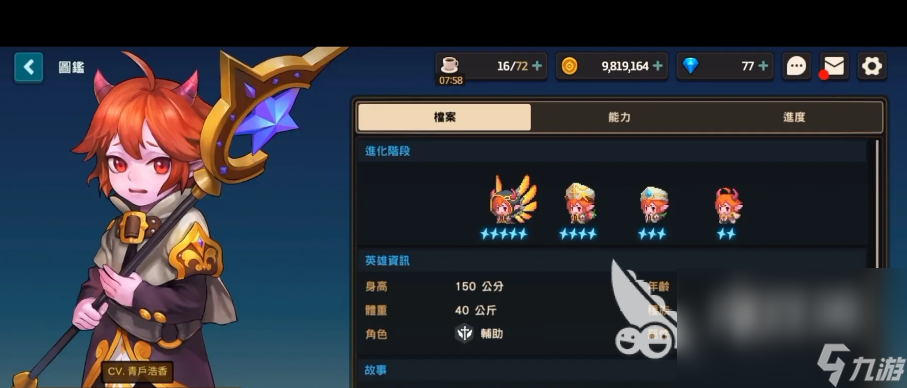
9、《公主连结》
高清的动画画质,玩游戏就好像看动漫那样欢乐,通过推动和欣赏剧情来养成角色,并且知道每个角色背后的故事,有条件的话还可以给角色更换时装打扮。
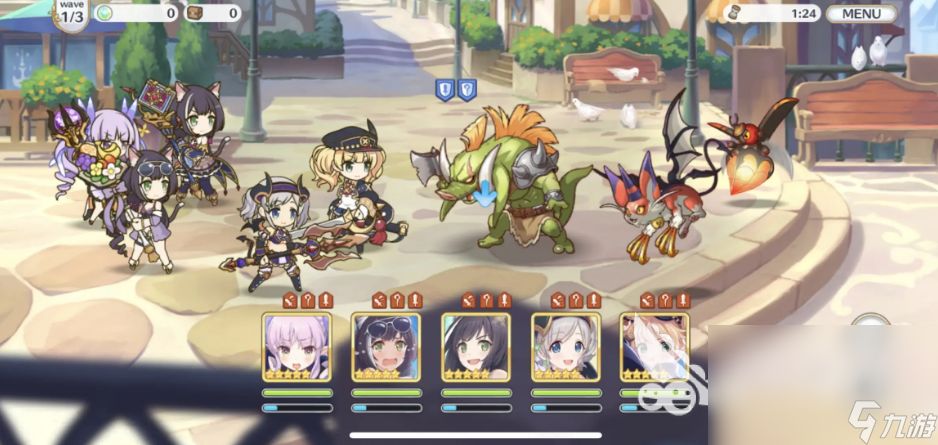
10、《偶像梦幻祭2》
可以听动感的音乐,然后再去养成这些活力少年们,百万字的剧情让大家看个过瘾,随着剧情的深入和少年一起同哭同笑,当少年在舞台上闪闪发光开演唱会的时候,就代表小伙伴养成成功了。

以上就是十大日系养成游戏排行榜2022推荐的内容了,每款游戏的主题都是不一样的,玩法也有所区别,大家可以挑选自己喜欢的来玩,来豌豆荚就能下载了。

 笨小笨
笨小笨












